On rectangles

While reading Cryptography: The Science of Secret Writing [1], the author makes a remark (p. 36) (without substantiating it further) that the number of possible distinct rectangles composed of squares (a regular grid) is quite limited.

Unsubstantiated (or, more exactly, undemonstrated) claims usually bug me if the demonstration is not immediate. In this case, I determined fairly rapidly the solution, but I guess I would have liked something less vague than “increased in size does not necessarily provide greater possibilities for combination.” Let’s have a look at that problem.

The problem is as follows: given , how many distinct rectangles with integer sides of surface are there?

The first observation one must make is that the solution depends on the integer factorization of . If then there’s obviously only one solution. If is prime, then there are only two solutions: and .

If is composite, then the first side must evenly divide (and thus uniquely determine the other side, ). What are the admissible divisors ? Let

be the prime divisors of , with multiplicities. For example, yields

which is readily verified.

Now, any side of length is the product of a subset of (with the empty subset understood as ); for example, for , is cromulent. The other side is uniquely determined, and is . Since one side is given by a subset and the other by the complement, we may have the idea that each subset corresponds to a bit-string:

yielding

This is sufficient to generate all permissible rectangles, but they are not all distinct just yet. This method does not permit to distinguish between

and, say,

…because both yield subsets whose products are the same: .

We must then account for indistinguishable subsets; fortunately, it’s simple once we have multiplicities, the number of times each prime factor appears. We find:

since . Let us now look at the relation between multiplicities and indistinguishable subsets. Let us just look at :

and the subsets (again, in “bitmask” notation”):

(a special case), then

and

and finally

There are 4 groups that yield distinct products. That’s , or the multiplicity of the first prime factor plus one. The same applies to the other prime factors; and finally, the number of rectangles is given by

where is the th multiplicity.

*
* *

Let’s see how we can use what we found to compute automatically the number of rectangles in everybody’s favorite language: C++. First, let us write a simple integer factorization function:

std::vector<int> factor_integer(int x)
 {
  std::vector<int> factors;

  int t=2;
  while (t<=x)
   if (x % t==0)
    {
     x/=t;
     factors.push_back(t);
    }
   else
    if (t>2)
     t+=2;
    else 
     t++;

  return factors;
 }

(An already much better way would have been to use a sieve of some sort; but let us not get into that just now.) Multiplicities are most easily found:

std::vector<int> count_multiplicities(const std::vector<int> & factors)
{
  std::vector<int> multiplicities;
  int m=1;

  for (int i=0;i<factors.size();i++)
    if (factors[i]==factors[i+1])
     m++;
    else
     {
      multiplicities.push_back(m);
      m=1;
     }


  return multiplicities;
}

finally:

int count_rectangles( const std::vector<int> & multiplicities )
 {
  int n=1;

  for (int i=0;i<multiplicities.size();i++)
   n*=(multiplicities[i]+1);

  return n;
 }

Then, to unit-test the thing (because, yes, testing is
important), an alternate implementation:

int enumerate_rectangles(const std::vector<int> & factors)
{
  std::map<rectangle,bool> seen;

  int c=(1<<factors.size());
  for (int i=0;i<c;i++)
   {
    int h=1;
    int w=1;
    int mask=i;
    for (int b=0;b<factors.size();b++,mask>>=1)
     {
      if (mask & 1)
       h*=factors[b];
      else
       w*=factors[b];
     }

    seen[ rectangle(h,w) ] = true;
   }

  return seen.size();
}

Let us check:

void show(const std::vector<int> & v)
{
  for_each( v.begin(),
            v.end(),
            [](int x) { std::cout << " " << x; } );
  std::cout << std::endl;
}

////////////////////////////////////////
int main()
{
  const int n = 2*2*3*3*5*7*13; // or whatever

  std::vector<int> factors=factor_integer(n);
  std::vector<int> multiplicities=count_multiplicities(factors);

  std::cout << "factors:"; show(factors);
  std::cout << "multiplicities:"; show(multiplicities);

  int enumerated=enumerate_rectangles(factors);

  std::cout
   << "enumerated: " << enumerated << std::endl
   << "computed: " << count_rectangles(multiplicities) << std::endl;

  return 0;
}

Running the program, we find, for example:

factors: 2 2 3 3 5 7 13
multiplicities: 2 2 1 1 1
enumerated: 72
computed: 72

*
* *

So all this because of a careless, unsubstantiated statement in an old book; I really wish such characterization, even when moderately interesting, would be explained and well-demonstrated. But now that we have all that we need, let’s have a look at the asymptotic-ish behavior.

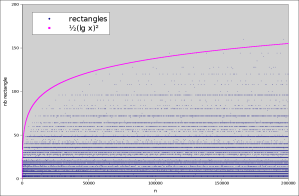
For from 1 to 200000, if we plot the number of rectangles:

The upper bound is . Well, there’s at most factors in a number (being exactly so when it is a power of two), and counting the average multiplicities, we have a rather good fit. Therefore, we can say (in a manner as vague as the original author that started this digression of a blog entry) what the number of possible rectangles for a given is .

[1] Laurence Dwight Smith — Cryptography: The Science of Secret Writing — Dover (1943)