Mathematics can ask you to remember things that have no obvious connection to common sense. Either because it’s arbitrary (the name of a function in respect to what it computes) or because you haven’t quite figured all the details out. In either cases, a few mnemonics are always useful!
The first series of mnemonics you’ll learn is to remember constants. Constants like and
have special importance in modern mathematics—beyond plain creepy piphilia.
The notation for is due to William Jones who first used it in print in 1707. He chose
probably because it had some mnemonic connection to perimeter, which make sense given the context. The notation was adopted and popularized by Euler, which in turn introduced the notation
for the base of the natural logarithm. It appeared in print in 1736.[1]
The constants and
are both transcendental irrational numbers.
The discipline of remembering digits of either—and of in particular—has risen to Olympic levels. For every day use knowing the values to 6 or 16 digits is probably quite sufficient1. To remember
to 20 digits, the following English poem does the trick:
3 Pie
141592 I wish I could determine Pi
65358 Eureka, cried the great inventor
9793 Christmas pudding, Christmas pie
23846 Is the problem’s very center
And, indeed, . For
, we have the same kind of poem:
2718281 We require a mnemonic to remember
And, indeed, quite so, . If you really want a whole lot of digits, you can have a look at Simon Plouffe‘s page of world records.
*
* *
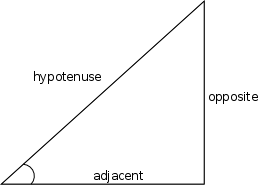
Trigonometric functions such as sine, cosine, and tangent are somewhat named arbitrarily. Maybe not tangent, because, more than the two others, it suggest something of a straight line, a slope. Fortunately, there’s a rather simple—if Japanese-sounding—mnemonic for those. Take a deep breath and say it out loud: SOHCAHTOA!
Indeed, sine is opposite over hypotenuse, cosine is adjacent over hypotenuse, and tangent is opposite over adjacent:
*
* *
Keeping up with a Japanese theme, a friend of mine, understanding nothing of the right-hand rule, came up with a simple mnemonic for remembering the vector cross product rules:
There’s also:
Let us look at a mitsudomoe crest:
You can imagine it spinning clockwise:
or counter-clockwise:

If the mitsudomoe is spinning clockwise, pen down ,
, and
in a clockwise manner:
If you read the products clockwise, the answer is the next vector clockwise. Indeed, .
The same works if you use it counter-clockwise: the answer is the next vector in counter-clockwise order: .
You can recompute the identities using the definition of cross-product based on the matrix determinant:
But that’s a lot of work.
*
* *
Mnemonics are always useful, if you manage to remember them. I mean it seriously. I think it’s easier to remember to 6 digits than to remember a 20-word poem. The clockwise/counter-clockwise analogy is a lot easier to remember if you’re a visual like I am.
*
* *
The Hidari Mitsudomoe images are based on a work released under the creative commons. The derived works complies with the license. The hiragana ‘sohcahtoa’ calligraphy is mine, I retain full rights on this image.
References
[1] Florian Cajori — A History of Mathematical Notations — Dover, 1993 (also available in two volumes: V.1 and V.2).
1 6–7 decimal digits corresponds to the safe precision of IEEE 754 float, 16 corresponds to double.





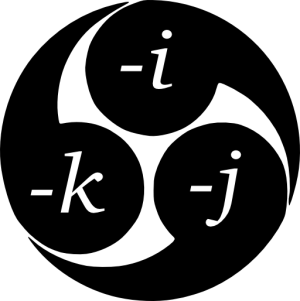
And, if you can remember e to 6 places, you’ve got it to 10 places.
True!
[…] Link via Harder, Better, Faster, Stronger. […]
This neat SOHCAHTOA video is great for inspiring your trig students.
ah ah that’s cute :p