Euclid, Primes numbers, and a Bit of Algorithm Analysis (Part IV)

While we looked at using the GCD for devising a Las Vegas-type algorithm to test for the primality of a number in a previous entry, we saw that actually testing the number against a list of primes (therefore assuming we have an arbitrarily long list of primes), one prime at a time, is much faster.

The GCD method, for divisor , tests a number in steps, but we haven’t determined the complexity of the other method. Let’s do that now.

Hash Table and Magic (Relatively Primes) Numbers

Today, let’s talk about hash tables. Or, more precisely, one type of secondary probing technique, one that uses some number theory—but not quadratic residues, just relatively prime numbers.

I don’t know if you’re like me, but it often bugs me when I read something in a textbook that seems to make sense, but is claimed without proof nor demonstration (oh, I think I said that before). That seems to happen particularly often when I read stuff about data structures, and this time I decided to explore one of those claims.

Amicable Numbers (Part II)

In the first part we discussed how to compute the sum of proper divisors function 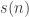from the sum of divisors function, . We saw that if we factorize the number then compute the list divisors from prime factor, it was much faster (on average) than testing each possible numbers from to (or 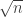, since we get one large divisor for every small divisors).

So now, let’s all put that together to get an efficient program that enumerates amicable pairs. First, we obtain a list of primes (not missing any) where the largest prime is , the largest number we will be testing—we need it to compute (up to) 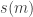. If we were to search for all amicable numbers, the list would need to be unbounded, maybe we would need to produce it as we go along; but if we look for amicable pairs up to, say, about 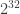, we only need primes up to 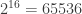(and there’sn’t that many of them). For the sake of efficiency, we also need a way of not testing a number twice.

The Sieve of Eratosthenes

The Ancient Greeks never fail to amaze me. Sometimes their ideas border the merely superstitious, sometimes you find a guy like Eratosthenes (c. 275 BC – c. 195 BC) that comes up with a truly modern idea. I’m not talking about his invention of geography (in the modern sense of the word) nor about his suspiciously accurate estimate of Earth’s size. No, I’m talking about an algorithm that has a very modern feel to it: the sieve of Eratosthenes

So what is it that I find so modern about this algorithm? Well, it has a computational feel to it, replacing smarts with a simple procedure, regular and repetitive. So, how hard is Eratosthenes’ sieve to implement? Not every: about 10 lines of code is needed in C++ (and possibly quite fewer if we use some other language).