31/01/2012
The float and double floating-point data types have been present for a long time in the C (and C++) standard. While neither the C nor C++ standards do not enforce it, virtually all implementations comply to the IEEE 754—or try very hard to. In fact, I do not know as of today of an implementation that uses something very different. But the IEEE 754-type floats are aging. GPU started to add extensions such as short floats for evident reasons. Should we start considering adding new types on both ends of the spectrum?

The next step up, the quadruple precision float, is already part of the standard, but, as far as I know, not implemented anywhere. Intel x86 does have something in between for its internal float format on 80 bits, the so-called extended precision, but it’s not really standard as it is not sanctioned by the IEEE standards, and, generally speaking, and surprisingly enough, not really supported well by the instruction set. It’s sometimes supported by the long double C type. But, anyway, what’s in a floating point number?
Read the rest of this entry »
 1 Comment |
1 Comment |  algorithms, C, C-plus-plus, data compression, data structures, hacks, machine learning, programming | Tagged: double, extended, float, IEEE 754, octuple, quadruple |
algorithms, C, C-plus-plus, data compression, data structures, hacks, machine learning, programming | Tagged: double, extended, float, IEEE 754, octuple, quadruple |  Permalink
Permalink
 Posted by Steven Pigeon
Posted by Steven Pigeon
24/01/2012
So in the two previous parts of this series, we have looked at the selection algorithm and at sorting networks for determining efficiently the (sample) median of a series of values.

In this last installment of the series, I consider an efficient (but approximate) algorithm based on heaps to compute the median.
Read the rest of this entry »
 7 Comments |
7 Comments |  algorithms, C, C-plus-plus, data structures, hacks, programming | Tagged: heap, max-heap, med-heap, median, min-heap, selection |
algorithms, C, C-plus-plus, data structures, hacks, programming | Tagged: heap, max-heap, med-heap, median, min-heap, selection |  Permalink
Permalink
 Posted by Steven Pigeon
Posted by Steven Pigeon
17/01/2012
Once upon a time, I discussed how to pick bit-rate for MP3, while considering re-ripping all my CDs. But if I’m to re-rip everything, I might as well do it one last time and use lossless compression.

In this post, we’ll discuss the simple script I cooked up to do just that, and a bit on how Flac works, and how it compares to MP3.
Read the rest of this entry »
 1 Comment |
1 Comment |  algorithms, Bash (Shell), data compression, embedded programming, Mathematics, programming | Tagged: CD, Entropy, Golomb Codes, GSM, Linear Prediction, music, psychoacoustic model, psychoacoustics, sound, Speech, Speech Codec |
algorithms, Bash (Shell), data compression, embedded programming, Mathematics, programming | Tagged: CD, Entropy, Golomb Codes, GSM, Linear Prediction, music, psychoacoustic model, psychoacoustics, sound, Speech, Speech Codec |  Permalink
Permalink
 Posted by Steven Pigeon
Posted by Steven Pigeon
15/01/2012
Tim Fitzharris — National Audubon Society Guide To Photographing National Parks (Digital Edition) — Firefly Books 2009, 192 pp. ISBN 978-1-55407-455-6

(Buy At Amazon.com)
Contrary to what the title may indicate, this book has little to do with actual digital photography techniques for landscapes or natural wonders; it is rather a tourist guide of everything you should see in the major american national parks. After expediting the basics of landscape photography, the guide leads you into a detailed journey into the United States major national parks, giving you all the good hints as to how to reach this-or-that natural wonder, what time of year, or even the time of day will lend itself the best for photography.
While this seems moderately interesting for a foreigner (especially if one doesn’t really want to visit all the state parks), the book is entirely redeemed by Fitzharris’ absolutely superb photography. A must get, especially if you’re interested in landscape photography.
 Leave a Comment » |
Leave a Comment » |  Suggested Reading | Tagged: Audubon, Landscape, National Audubon, National Parks, Photography |
Suggested Reading | Tagged: Audubon, Landscape, National Audubon, National Parks, Photography |  Permalink
Permalink
 Posted by Steven Pigeon
Posted by Steven Pigeon
15/01/2012
William Gurstelle — The Practical Pyromaniac: Build Fire Tornadoes, One-Candlepower Engines, Great Balls of Fire, and More Incendiary Devices — Chicago Review Press, 2011, 212 pp. ISBN 978-1-56976-710-8

(Buy At Amazon)
This book is quite the step up from Mini Weapons Of Mass Destruction 2: not only the projects presented are a lot more interesting—flame-thrower and all—they are presented in their historical and scientific contexts, explaining the active principles of each device/contraption. While Mini Weapons was something of a kid’s book, The Practical Pyromaniac certainly isn’t. I must say it will appeal quite a lot to every one with a little envie de destruction.
 Leave a Comment » |
Leave a Comment » |  Suggested Reading | Tagged: flame-thrower, mischief, pyromaniac |
Suggested Reading | Tagged: flame-thrower, mischief, pyromaniac |  Permalink
Permalink
 Posted by Steven Pigeon
Posted by Steven Pigeon
10/01/2012
In the previous post of this series, we left off where we were asking ourselves if there was a better way than the selection algorithm of finding the median.

Computing the median of three numbers is a simple as sorting the three numbers (an operation that can be done in constant time, after all, if comparing and swapping are constant time) and picking the middle. However, if the objects compared are “heavy”, comparing and (especially) moving them around may be expensive.
Read the rest of this entry »
 4 Comments |
4 Comments |  algorithms, C, C-plus-plus, data structures, programming | Tagged: ADL, cmpxchg, median, Sorting Networks |
algorithms, C, C-plus-plus, data structures, programming | Tagged: ADL, cmpxchg, median, Sorting Networks |  Permalink
Permalink
 Posted by Steven Pigeon
Posted by Steven Pigeon
03/01/2012
The usual way of forming a search tree from a list is to scan the list and insert each of its element, one by one, into the tree, leading to a(n expected) run-time of  .
.

However, if the list is sorted (in ascending order, say) and the tree is not one of the self-balancing varieties, insertion is 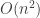 , because the “tree” created by the successive insertions of sorted key is in fact a degenerate tree, a list. So, what if the list is already sorted and don’t really want to have a self-balancing tree? Well, it turns out that you can build a(n almost perfectly) balanced tree in
, because the “tree” created by the successive insertions of sorted key is in fact a degenerate tree, a list. So, what if the list is already sorted and don’t really want to have a self-balancing tree? Well, it turns out that you can build a(n almost perfectly) balanced tree in 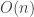 .
.
Read the rest of this entry »
 6 Comments |
6 Comments |  algorithms, data compression, data structures, programming | Tagged: Compact Tree, Compact Tree Storage, Huffman, Huffman Codes, phase-in codes, Search Tree, Segregated Storage, Tree |
algorithms, data compression, data structures, programming | Tagged: Compact Tree, Compact Tree Storage, Huffman, Huffman Codes, phase-in codes, Search Tree, Segregated Storage, Tree |  Permalink
Permalink
 Posted by Steven Pigeon
Posted by Steven Pigeon




 Posted by Steven Pigeon
Posted by Steven Pigeon 





