Size(_t) matters!

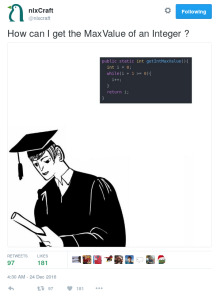
Sometime last week, a tweet from @nixCraft prompted the question, quite ironically, how do you get the maximum (largest positive) value for an integer?

π, π, Archimedes!

This week, another derivation for a famous formula: Archimedes’
formula for π.

Some time in the 3rd century BC, Archimedes used the perimeter of a regular polygon, starting with an hexagon and repeatedly doubling the number of sides, to estimate the value for π. He arrived at the approximation

.

How he arrived to this result is a bit mysterious until we completely understand how he got that result. Let’s see together how he did it.

Binet’s Formula

You will encounter a large number of formulas in your life, and quite many of them just seem to come out of the blue. That’s fortunately quite false, despite it being not always easy to retrace the formulas’ authors’ steps. One that appears as suspicious as it seems magic, is Binet’s Fibonacci Number formula:

,

where

is the golden number.

But it’s not quite out of nowhere, and, if you know how to solve recurrences using the characteristic equation, it’s in fact quite straightforward. Let’s see how.

Pretty Printing a Tree in a Terminal

More often than I’d like, simple tasks turn out to be not that simple. For example, displaying (beautifully) a binary tree for debugging purpose in a terminal. Of course, one could still use lots of parentheses, but that does not lend itself to a very fast assessment of the tree. We could, however, use box drawing characters, as in DOS’s goode olde tymes, since they’re now part of the Unicode standard.