It’s been a while since I last talked about data compression. Let us return to the topic this week with universal codes. Universal codes are entropy-like codes, but, unlike, say, Huffman codes, they presuppose very little on the distribution of the integers to code.

We can use optimally a universal code for a random variable  if
if
We will show how to build an universal code in a moment, but we will first state the condition that makes a code universal if the probability distribution satisfies the above condition. A code with length function  (the length of the code for the integer
(the length of the code for the integer  ) is
) is  -universal if, and only if
-universal if, and only if
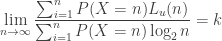
That is, the expectation of the length (in bits) of the code is proportional to the logarithm of the number being coded.
Let’s now see what an universal code looks like
Read the rest of this entry »
, which are pretty much as good as it gets.



 Posted by Steven Pigeon
Posted by Steven Pigeon 