A random Golden Ratio Appears!

Well, we all make errors once in a while, but sometimes they’re more interesting than others. So I inadvertently forgot a square in a calculation and the series suddenly started converging, to the most beautiful of convergences of all: .

So, let’s see how I got the golden ratio to emerge from a broken algorithm.

First, I wrote the recurrence as (remember, I forgot a square out somewhere):

The first few terms of the series:

,

,

,

,

,

,

,…

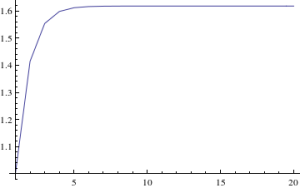
and if you plot them, you see that they do converge rapidly:

And the value 1.61-ish should be familiar. Could it converge to the golden ratio,

?

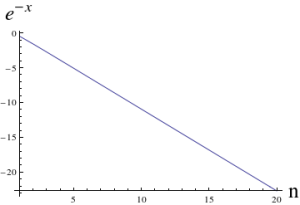
Well, numerically it does. Very quickly. The following log-plot shows the error :

Empirically, we are now fairly convinced that the limit of as goes to infinity is . Can we show it algebraically? Yes! And, no, it wont be überschmerzlich¹.

Let

Let’s square it, and see what happens:

So it’s…

and we find that the unique that satisfies the above equation is

and therefore,

.

---

¹ Superpainful.